Some questions and sections in an RFx survey or questionnaire are more important than others. This relative importance should be reflected when total scores are calculated for the vendors being assessed. PostRFP allows evaluators to set weights for both questions and sections, and can then calculate weighted totals using one of two possible scoring formulas.
In PostRFP, all questions are scored on the same scale (1-10 by default). Each question is then given a weighting which can be any positive whole number. By default, the weighting for a question is 1. Most questionnaires are organised into a structure of sections and sub sections, so PostRFP allows further weightings to be allocated to sections.
When a survey consists of sections and subsections (nested to any depth), with weights applied at both question and section level, the mathematics for deriving a total score for each vendor becomes surprisingly complex and error prone when calculated in a spreadsheet. Two alternative scoring formulas are supported by PostRFP.
For example, consider the following example RFP questionnaire for evaluating Hotels:
1 Location (1)
1.1 Distances From Key Locations (2)
1.2 Mini bus collection (1)
2 Services (1)
2.1 Swimming Pool? (1)
2.2 How many bars? (1)
2.3 Health Club? (1)
3 Pricing (2)
3.1 Standard Room Rate (1)
3.2 Deluxe Room Rates (1)
The figures in brackets show the weighting allocated to each section and question. These weightings are applied when calculating total scores for each Supplier's answered response. PostRFP supports two different formulas for calculating Total weighted scores:
- Arithmetic
- Normalised
Arithmetic Scoring Formula
This is the simplest formula. The total score for a respondent is found as follows:- Calculate the question score X question weight for each answered question
- Sum the weighted question scores for each section, then multiply by the section weight
- Sum the weighted section scores to find the total score.
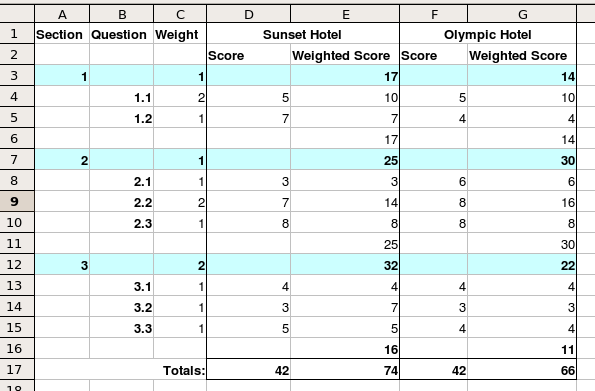
This is a simple way to calculate the totals. In summary, questions scores are multiplied by question weights and section weights, and then summed to produce a total score.
As described above, the crucial thing about Arithmetic scoring is that increasing the weighting for a question has the effect of increasing the contribution that the parent section makes to the total questionnaire score. In other words, the Section weighting does not alone describe the contribution of that section to the questionnaire as a whole. In order to separate the effect of question and section weighting we need to normalise the scores for each section and subsection
Normalised Scoring Formula
Normalising the scores converts the weighted score for each answer in a section to the percentage of the total possible score for that section. So the total possible score for a section is 100%. Therefore, with Normalised totals, Section weightings define and cap the contribution that a given section can make to the total questionnaire score.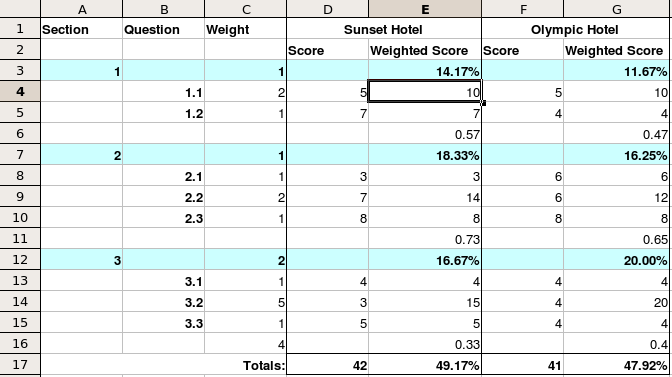

Comments